Passo a passo para construção do gráfico da função do segundo grau

Matemática

No Ensino Fundamental, funções são fórmulas matemáticas que associam cada número de um conjunto numérico (o domínio) a um único número pertencente a outro conjunto (o contradomínio). Quando essa fórmula é uma equação do segundo grau, temos uma função do segundo grau.

As funções podem ser representadas por figuras geométricas cujas definições coincidem com suas fórmulas matemáticas. É o caso da reta, que representa funções do primeiro grau, e da parábola, que representa funções do segundo grau. Essas figuras geométricas são chamadas de gráficos.

A ideia central da representação de função por um gráfico

Para desenhar o gráfico de uma função, é preciso avaliar qual elemento do contradomínio está relacionado com cada elemento do domínio e marcá-los, um a um, em um plano cartesiano. Quando todos esses pontos forem marcados, o resultado será justamente o gráfico de uma função.

Vale ressaltar que as funções do segundo grau, geralmente, são definidas em um domínio igual a todo o conjunto dos números reais. Esse conjunto é infinito e, por isso, é impossível marcar todos os seus pontos em um plano cartesiano. Desse modo, a alternativa é esboçar um gráfico que possa representar em parte a função avaliada.

Antes de qualquer coisa, lembre-se de que as funções do segundo grau possuem a seguinte forma:

y = ax² + bx + c

Diante disso, apresentamos cinco passos que tornam possível a construção de um gráfico de função do segundo grau, exatamente como os que são exigidos no Ensino Médio.

Passo 1 – Avaliação geral da função

Existem alguns indicadores que ajudam a descobrir se o caminho certo está sendo tomado ao construir o gráfico de funções do segundo grau.

I - O coeficiente “a” de uma função do segundo grau indica sua concavidade, ou seja, se a > 0, a parábola será para cima e possuirá ponto de mínimo. Se a < 0, a parábola será para baixo e possuirá ponto de máximo.

II) O primeiro ponto A do gráfico de uma parábola pode ser facilmente obtido apenas observando o valor do coeficiente “c”. Desse modo, A = (0, c). Isso ocorre quando x = 0. Observe:

y = ax² + bx + c

y = a·0² + b·0 + c

y = c

Passo 2 – Encontrar as coordenadas do vértice

O vértice de uma parábola é o seu ponto de máximo (se a < 0) ou de mínimo (se a > 0). Ele pode ser encontrado pela substituição dos valores dos coeficientes “a”, “b” e “c” nas fórmulas:

x_v = – b
       2a

y_v = – ∆
        4a

Desse modo, o vértice V é dado pelos valores numéricos de x_v e y_v e pode ser escrito assim: V = (x_v,y_v).

Passo 3 – Pontos aleatórios do gráfico

É sempre bom indicar alguns pontos aleatórios cujos valores atribuídos à variável x sejam maiores e menores que x_v. Isso lhe dará pontos antes e depois do vértice e tornarão o desenho do gráfico mais fácil.

Passo 4 – Se possível, determine as raízes

Quando existem, as raízes podem (e devem) ser incluídas no desenho do gráfico de uma função do segundo grau. Para encontrá-las, faça y = 0 para obter uma equação do segundo grau que possa ser resolvida pela fórmula de Bhaskara. Lembre-se de que resolver uma equação do segundo grau é o mesmo que encontrar suas raízes.

A fórmula de Bhaskara depende da fórmula do discriminante. São elas:

x = – b ± √∆
     2a

∆ = b² – 4ac

Passo 5 – Marcar todos os pontos obtidos no plano cartesiano e ligá-los, de modo a construir uma parábola

Lembre-se de que o plano cartesiano é formado por duas retas numéricas perpendiculares. Isso significa que, além de conter todos os números reais, essas retas formam um ângulo de 90°.

Exemplo de plano cartesiano e exemplo de parábola.

Exemplo

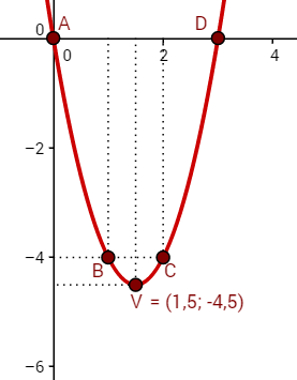
Construa o gráfico da função do segundo grau y = 2x² – 6x.

Solução: Observe que os coeficientes dessa parábola são a = 2, b = – 6 e c = 0. Dessa maneira, pelo passo 1, podemos afirmar que:

1 – A parábola ficará para cima, pois 2 = a > 0.

2 – Um dos pontos dessa parábola, representado pela letra A, é dado pelo coeficiente c. Logo, A = (0,0).

Pelo passo 2, observamos que o vértice dessa parábola é:

x_v = – b
      2a

x_v = – (– 6)
     2·2

x_v = 6
      4

x_v = 1,5

y_v = – ∆
        4a

y_v = – (b² – 4·a·c)
      4·a

y_v = – ((– 6)² – 4·2·0)
     4·2

y_v = – (36)
         8

y_v = – 36
         8

y_v = – 4,5

Logo, as coordenadas do vértice são: V = (1,5, – 4,5)

Utilizando o passo 3, escolheremos apenas dois valores para a variável x, um maior e outro menor que x_v.

Se x = 1,

y = 2x² – 6x

y = 2·1² – 6·1

y = 2·1 – 6

y = 2 – 6

y = – 4

Se x = 2,

y = 2x² – 6x

y = 2·2² – 6·2

y = 2·4 – 12

y = 8 – 12

y = – 4

Logo, os dois pontos obtidos são B = (1, – 4) e C = (2, – 4)

Pelo passo 4, que não precisa ser feito caso a função não possua raízes, obtemos os seguintes resultados:

∆ = b² – 4ac

∆ = (– 6)² – 4·2·0

∆ = (– 6)²

∆ = 36

x = – b ± √∆
     2a

x = – (– 6) ± √36
  2·2

x = 6 ± 6
     4

x' = 12
      4

x' = 3

x'' = 6 – 6
     4

x'' = 0

Logo, os pontos obtidos por meio das raízes, tendo em vista que, para obter x = 0 e x = 3, foi preciso fazer y = 0, são: A = (0, 0) e D = (3, 0).

Com isso, obtemos seis pontos para desenhar o gráfico da função y = 2x² – 6x. Agora basta cumprir o passo 5 para construí-lo definitivamente.

Por Luiz Paulo Moreira
Graduado em Matemática

(Fonte: Brasil Escola)