ORIGEM DOS SINAIS

ORIGEM DOS SINAIS

    Adição ( + ) e subtração ( - )

    O emprego regular do sinal + ( mais ) aparece na Aritmética Comercial de João Widman d'Eger publicada em Leipzig em 1489.
Entretanto, representavam não à adição ou à subtração ou aos números positivos ou negativos, mas aos excessos e aos déficit em problemas de negócio. Os símbolos positivos e negativos vieram somente ter uso geral na Inglaterra depois que foram usados por Robert Recorde em 1557.Os símbolos positivos e negativos foram usados antes de aparecerem na escrita. Por exemplo: foram pintados em tambores para indicar se os tambores estavam cheios ou não.

    Os antigos matemáticos gregos, como se observa na obra de Diofanto, limitavam-se a indicar a adição juntapondo as parcelas - sistema que ainda hoje adotamos quando queremos indicar a soma de um número inteiro com uma fração. Como sinal de operação mais usavam os algebristas italianos a letra P, inicial da palavra latina plus.

    Multiplicação ( . ) e divisão ( : )

    O sinal de X, como que indicamos a multiplicação, é relativamente moderno. O matemático inglês Guilherme Oughtred empregou-o pela primeira vez, no livro Clavis Matematicae publicado em 1631. Ainda nesse mesmo ano, Harriot, para indicar também o produto a efetuar, colocava um ponto entre os fatores. Em 1637, Descartes já se limitava a escrever os fatores justapostos, indicando, desse modo abreviado, um produto qualquer. Na obra de Leibniz escontra-se o sinal 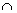para indicar multiplicação: esse mesmo símbolo colocado de modo inverso indicava a divisão.

    O ponto foi introduzido como um símbolo para a multiplicação por G. W. Leibniz. Julho em 29, 1698, escreveu em uma carta a John Bernoulli: "eu não gosto de X como um símbolo para a multiplicação, porque é confundida facilmente com x; freqüentemente eu relaciono o produto entre duas quantidades por um ponto . Daí, ao designar a relação uso não um ponto mas dois pontos, que eu uso também para a divisão."
As formas a/b e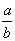 , indicando a divisão de a por b, são atribuídas aos árabes: Oughtred, e, 1631, colocava um ponto entre o dividendo o divisor. A razão entre duas quantidades é indicada pelo sinal :, que apareceu em 1657 numa obra de Oughtred. O sinal ÷, segundo Rouse Ball, resultou de uma combinação de dois sinais existentes - e :

    Sinais de relação ( =, < e > )

    Robert Recorde, matemático inglês, terá sempre o seu nome apontado na história da Matemática por ter sido o primeiro a empregar o sinal = ( igual ) para indicar igualdade. No seu primeiro livro, publicado em 1540, Record colocava o símbolo 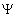entre duas expressões iguais; o sinal = ; constituído por dois pequenos traços paralelos, só apareceu em 1557. Comentam alguns autores que nos manuscritos da Idade Média o sinal = aparece como uma abreviatura da palavra est.

    Guilherme Xulander, matemático alemão, indicava a igualdade , em fins do século XVI, por dois pequenos traços paralelos verticais; até então a palavra aequalis aparecia, por extenso, ligando os dois membros da igualdade.

    Os sinais > ( maior que ) e < ( menor que ) são devidos a Thomaz Harriot, que muito contribuiu com seus trabalhos para o desenvolvimento da análise algébrica.
(Fonte: voc e sabia.net)