Curiosidades sobre os números

Curiosidades sobre os números

As curiosidades sobre os números são propriedades matemáticas que podem ser usadas para a diversão ou como passatempo para os amantes dessa disciplina.

Publicado por: Luiz Paulo Moreira Silva 

Algumas propriedades dos números podem ser usadas como passatempo ou diversão

A Matemática é a ciência que estuda as relações existentes entre números, formas geométricas, figuras, funções etc. Essas relações foram criadas para ajudar o ser humano a resolver problemas cotidianos e depois evoluíram para relações usadas apenas para a própria Matemática. Nesse processo, é possível perceber algumas curiosidades sobre os objetos criados por esse campo de estudo.

Neste artigo, mostramos algumas curiosidades interessantes sobre os números que estão no conjunto de relações matemáticas criadas apenas para a própria Matemática, ou seja, sem o objetivo de serem usadas efetivamente para resolver problemas.

Número mágico

O número 1089 ficou conhecido como número mágico por um motivo bem óbvio: 1089 é um número mágico.

Para perceber isso, anote um número qualquer que possua três algarismos diferentes, por exemplo, 123. Escreva esse mesmo número ao contrário e subtraia o menor do maior:

321 – 123 = 198

Agora, some o resultado da subtração com o inverso desse número:

198 + 891 = 1089

Essa “propriedade” é válida para qualquer número com três dígitos diferentes.

Números triangulares

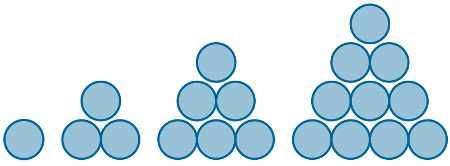
Números triangulares são naturais que representam quantidades que podem ser organizadas na forma de triângulo equilátero. Exemplos: 1, 3, 6 e 10. Observe os triângulos equiláteros que podem ser formados por esses números:

A sequência de números triangulares não para aí: é infinita! Para encontrar um número triangular qualquer, podemos continuar desenhando os triângulos equiláteros e contando seus elementos, ou usar a seguinte fórmula:

Tn = n(n + 1)
      2

Nessa fórmula, n é a “posição” do número triangular. Assim, o quarto número triangular é 10, logo n = 4. Se quisermos encontrar o vigésimo número triangular, basta substituir n por 20 na fórmula.

Encontrando o próximo quadrado perfeito

Sabendo que 144 é um quadrado perfeito, como encontrar o próximo? A maneira mais conhecida é calcular a raiz quadrada desse número, que é 12, e elevar o próximo número natural ao quadrado, obtendo 13² = 169. Entretanto, usando produtos notáveis, é possível perceber uma propriedade interessante. O quadrado da soma é:

(a + b)² = a² + 2ab + b²

Se queremos descobrir qual é o quadrado de 13, sabendo que 12² = 144, basta notar que 13 = 12 + 1 e usar os produtos notáveis:

(a + b)² = a² + 2ab + b²

(12 + 1)² = 12² + 2·12·1 + 1²

(13)² = 12² + 2·12 + 1

13² = 169

Note que é possível construir uma propriedade com essa técnica. Se x² é um quadrado perfeito, então o próximo quadrado perfeito pode ser obtido com:

(x + 1)² = x² + 2x + 1

Raízes de quadrados perfeitos

O número 144 é um quadrado perfeito, pois:

√144 = 12

Invertendo os algarismos desse quadrado perfeito, obtemos 441, cuja raiz é:

√441 = 21

Essa propriedade não funciona para todo quadrado perfeito, mas é interessante saber que existam números assim e descobri-los pode ser um bom passatempo.

Forma pitagórica de calcular potências

Observe a sequência:

1² = 1

2² = 1 + 3

3² = 1 + 3 + 5

4² = 1 + 3 + 5 + 7

5² = 1 + 3 + 5 + 7 + 9

…

É evidente que a forma pitagórica de calcular quadrados é baseada na soma de números ímpares. Se a potência for 10², por exemplo, somamos os 10 primeiros números ímpares.

Note que os números ímpares formam um a progressão aritmética de razão 2. Assim, podemos fazer a soma dos termos finitos de uma PA de razão 2, n termos e a₁ = 1 para determinar qual será o quadrado de um número de base n e expoente 2.

Assim, temos:

n² = n(a₁ + a_n)
      2

Entretanto, antes de fazer essa soma, é necessário descobrir qual é o último número ímpar da sequência, o que pode ser feito pela seguinte fórmula:

a_n = a₁ + (n – 1)r

Nessa fórmula, r é a razão da PA e a_n seu último termo, ou seja, o número que queremos descobrir.

Assim, para calcular 223², podemos fazer:

a_n = a₁ + (n – 1)r

a_n = 1 + (223 – 1)2

a_n = 1 + (222)2

a_n = 1 + 444

a_n = 445

Em seguida, faremos:

223² = n(a₁ + a_n)
        2

223² = 223(1 + 445)
          2

223² = 223·446
          2

223² = 99458
         2

223² = 49729

(Fonte: Mundo Educação)